There are various problem types one can face. Some of them are easily solvable; some don’t have a solution at all. And having a computer won’t necessarily help. In this blog post, I am going to explore three problems solving (relaxation) approaches: constraint, continuous and Lagrangian relaxation methods.
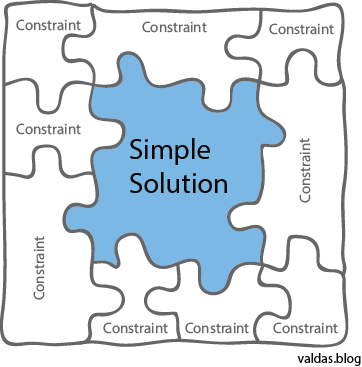
Constraint Relaxation: Look for the simplest solution to a problem and add constraints
Or in other words, what would this look like if it were easy?
Constraint Relaxation technique suggests to remove some of the problem’s constraints and solve a problem we wish we had. Then, after we’ve made progress, try to add the restrictions back in. Make the problem easier to handle before bringing it to back to reality. As a result, it might become evident that you were about to overengineer from the beginning. In some cases, adding constraints will not be possible. But fortunately, now you understand the problem much better, which puts you in a better position to solve it more efficiently.
“More things should not be used than are necessary.” - William of Ockham
William of Ockham made a principle, nowadays known as Occam’s razor, which states that if there are several possible ways that something might have happened, the idea that uses the fewest guesses is probably the right one.
Continuous Relaxation: Turn binary choices into continua
In many problems there no shades of gray in between - you go either one way or another. But we can use probabilities to decide what may be the best option for us. Imagine you are about to choose a movie for a night, deciding between Start Wars The Last Jedi and The Fate of the Furious (can’t watch two movies at the same time). First, imagine a 50 - 50 blend and then round it up or down; based on IMDB ratings, reviews, whatever factors that are relevant to you. Finally, probabilities differ, and it becomes clear what movie you should watch.


If there’s no smooth continuum among solutions, make a scoring system and choose the winner.
Lagrangian Relaxation: Bend the rules and accept the consequences
Anything is possible if you pay the price.
The third, Lagrangian Relaxation, turns impossibilities into penalties, teaching the art of breaking the rules and accepting the consequences. Let’s take as an example the project management triangle, which is a model of the constraints in project management.
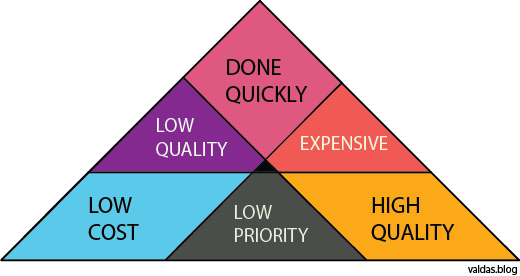
- The quality of work is constrained by the cost, deadlines, and scope (features).
- The project manager can trade between constraints.
- Changes in one constraint necessitate changes in others to compensate, or quality will suffer.
Which things are you ready to sacrifice to solve a problem?
If you are interested in other algorithms to apply in daily life, read Algorithms to Live By: The Computer Science of Human Decisions. Here is my blog post with the key insights.

Links: Lagrangian relaxation Penalty method Algorithms to Live By: The Computer Science of Human Decisions
